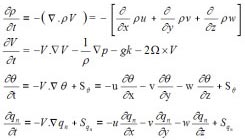Si alguien se plantea antes de un viaje cuando llegará a su destino, tendrá en cuenta a qué velocidad va a desplazarse y qué distancia debe recorrer, de forma que si su velocidad va a ser de 60 Km/h y va a recorrer 120 Km, sabe que empleará dos horas en llegar. Aunque cueste creerlo, este sencillo cálculo se basa en nuestro conocimiento sobre las leyes físicas que rigen el sistema (el coche y la carretera), en particular, sobre la mecánica newtoniana y concretamente sobre las leyes del movimiento mecánico, es decir, sabemos que espacio recorrido es igual a velocidad por tiempo (matemáticamente se expresa a través de la ecuación e=v.t), por lo que una vez despejado el tiempo (t=e/v) calcularemos cuál será el tiempo empleado (120/60=2). Como el planteamiento lo hacemos antes del viaje, realmente estamos pronosticando algo que ocurrirá en el futuro, es decir que si salimos a las 7 llegaremos a cenar a las 9.

Si alguien se plantea cuál será el tiempo mañana, se pregunta sobre cuál será la temperatura, la humedad, velocidad del viento y el valor de otra serie de variables meteorológicas que caracterizan el estado atmosférico. La respuesta la encontrará en base al conocimiento del sistema La atmósfera es básicamente un fluido turbulento, por lo que responde a las leyes de la mecánica de fluidos y obviamente no podemos aplicar ecuaciones tan sencillas como las que respondían a la cuestión anterior. No obstante, el problema de la predicción numérica del tiempo guarda ciertas simetrías con el de nuestro viaje en coche, como veremos a continuación.

Conseguir una buena predicción del tiempo es el resultado de un proceso complejo en el que se deben considerar distintos principios físicos y técnicas numéricas, así como disponer de una buena caracterización del estado inicial del sistema. Antes de proceder a exponer los aspectos más relevantes de la predicción numérica del tiempo, vamos a hacer alguna consideración previa sobre simulaciones y modelos.

Simulaciones y modelos

Una simulación es el proceso mediante el cual reproducimos el comportamiento de un sistema a partir de un modelo. Un modelo es una abstracción de la realidad que captura la esencia funcional del sistema real, con el detalle suficiente como para que pueda representarlo en una aplicación concreta. En el caso que nos ocupa la finalidad de una simulación atmosférica es aumentar la comprensión sobre los procesos físicos que gobiernan la atmósfera.
Si el conocimiento que requerimos del sistema es cualitativo podríamos recurrir a los denominados modelos físicos, basados en la representación del sistema a escala a través de una maqueta que se introduce en túneles de viento, tanques u otro tipo de dispositivos en condiciones de similitud. Si el conocimiento que necesitamos del sistema es cuantitativo podremos recurrir a un modelo matemático. Estos modelos están basados en la representación del comportamiento del sistema a través de la solución del conjunto de ecuaciones que lo gobiernan. Los modelos matemáticos de tipo analítico permiten obtener soluciones exactas, lo que en la práctica implica, bien que el sistema a modelar es extremadamente simple, bien que las ecuaciones planteadas sólo lo representan de forma simplificada. Un modelo numérico se basa en la utilización de técnicas numéricas para la resolución computacional aproximada, del conjunto completo de ecuaciones que describen el sistema. En casi todas las situaciones reales que se plantean a la hora de simular la atmósfera, deberemos optar por la segunda opción, es decir, por un modelo matemático numérico que posibilite la resolución de las ecuaciones simultáneas, no lineales en derivadas parciales que describen la atmósfera.

De acuerdo con las escalas espaciales a las que se aplican, los modelos meteorológicos se pueden clasifican en tres grandes bloques; los modelos globales los modelos regionales (o de mesoescala) y los modelos de microescala. Los primeros se encargan fundamentalmente de la predicción numérica del tiempo a escala planetaria o en los estudios de cambio climático; los modelos regionales son los que sirven para reproducir fenómenos de mesoescala y predecir el "tiempo local", los modelos de microescala se diseñan para simular fenómenos turbulentos y superficiales de especial interes en la simulación de dispersión de contaminantes. En base a la especificación del contorno del modelo tenemos modelos de circulación general GCM (General Circulation Models): que cubren todo el planeta y modelos LAM (Límited área Models): que cubren solamente un área limitada. A menudo un sistema de predicción operativo dispone de modelos LAM anidados dentro de modelos GCM. Los modelos globales se emplean para reproducir las características sinópticas de la atmósfera, mientras que se aplican modelos LAM para afinar las predicciones hasta reproducir las características de las circulaciones y procesos atmosféricos locales. Los modelos de área limitada suelen aplicar técnicas de resolución basadas en diferencias finitas, mientras que los modelos globales suelen emplear algún tipo de técnica espectral, especialmente adecuada en ausencia de bordes.

Un poco de historia

El primer intento de predicción numérica del tiempo se debe al científico británico L.F. Richardson, quien en 1922 mostró como las ecuaciones diferenciales que gobiernan los movimientos atmosféricos pueden enunciarse de forma aproximada como un conjunto de ecuaciones en diferencias algebraicas para los valores de las tendencias de varias variables de campo en un número finito de puntos del espacio. Dados estos valores observados se podían calcular las tendencias numéricamente resolviendo las ecuaciones en diferencias para posteriormente extrapolarlas a un periodo de tiempo de forma que obtenemos un campo futuro con el cual podemos repetir el proceso obteniendo una predicción. Los intentos de llevar a la práctica este método en aquellos tiempos de escasez de datos experimentales y cálculos manuales no dieron buenos resultados.

Así, el interés por la predicción numérica del tiempo fue decayendo hasta que en los años 50 la gran expansión de observaciones meteorológicas y el desarrollo de los computadores propició el nacimiento del primer modelo meteorológico numérico que tuvo éxito en la predicción del tiempo, el denominado modelo barotrópico, modelo cuyas ecuaciones de movimiento eran mucho más simplificadas (ecuación de vorticidad y divergencia simplificadas aplicadas al nivel de divergencia nula) que el planteamiento inicial de Richardson (ecuaciones de movimiento completas). Este primer modelo suministraba predicciones del geopotencial a 500 mb . A este modelo le siguió el barotrópico modificado, que introducia una corrección empírica para la divergencia de onda larga. Posteriormente aparecen los modelos baroclínicos que se aplican a dos capas atmosféricas (basados en la aplicación de la ecuación de vorticidad a dos niveles y una evaluación del término de divergencia), y sobre todo a análisis vista su poca capacidad predictiva. No es hasta 1962 cuando se desarrolla un modelo de predicción realmente operativo denominado modelo geostrófico basado en un modelo baroclínico filtrado de tres niveles, que será mejorado y extendido a más niveles en años sucesivos.

Las limitaciones de aplicación de las ecuaciones de vorticidad barotrópicas, hizo que la evolución de los modelos sinópticos tomara el camino de las ecuaciones primitivas expresadas en coordenadas de presión, es decir, la consideración de un sistema no lineal de tres ecuaciones de pronóstico (componentes x e y de la ecuación de movimiento y la energía termodinámica) y tres ecuaciones de diagnóstico (la ecuación de continuidad, la aproximación hidrostática y la ecuación de estado), expresado en coordenadas isobáricas.

De este modo, empezaron a aparecer modelos de ecuaciones primitivas operativos en base a distintas técnicas numéricas y distintas distribuciones de estratos. El primero de todos fue un modelo de ecuaciones primitivas (EP) con seis niveles verticales, con dominio hemisférico, que fue operativo en el Centro Meteorológico Nacional de los Estados Unidos en 1966. Es en ese momento cuando la disponibilidad de medidas, la mejora en las técnicas de inicialización y la disponibilidad de recursos computacionales permite el nacimiento, a partir del modelo hemisférico, del primer modelo de área limitada de escala regional. Este modelo se introduce en 1971 y se denomina modelo LFM (Limited-area Fine Mesh). Este modelo incrementaba la resolución horizontal sobre el área de Norteamérica, área en la que se pretendía afinar la predicción sinóptica.

A partir de este modelo se desarrolló en 1975 el modelo MFM (Movable Fine Mesh), modelo de alta resolución que permitía el movimiento de la rejilla más fina de forma que se podía "enfocar" sobre el área de interés (como movimiento de huracanes o zonas de intensa precipitación). Paralelamente a este refinamiento del que surgen los primeros modelos "regionales" que podemos considerar de mesoescala, el modelo hemisférico de EP va sufriendo sucesivas mejoras en su capacidad de predicción sinóptica, hasta que es sustituido en 1980 por un modelo global de Ecuaciones Primitivas de 12 niveles que se resuelve mediante técnicas espectrales (en vez de hemisférico y resuelto con técnicas de puntos de rejilla) que permite predecir fenómenos de gran escala como la evolución de ondas baroclínicas (>2000Km) para periodos de 5 a 10 días.

A partir de los 80, cuando el acceso a los recursos computacionales se facilita substancialmente, se propicia una explosión en la simulación numérica de mesoescala, apareciendo multitud de modelos con distintas parametrizaciones y soluciones numéricas. A partir de ese instante, las grandes instituciones y universidades comienzan a recoger los frutos de los distintos modelos experimentales que van desarrollándose y adquiriendo la calidad suficiente para convertirse en muchos casos en modelos operativos de predicción.

El estado inicial

Una de las claves para que a través de las ecuaciones lleguemos al pronóstico correcto, es la determinación adecuada del estado inicial. Nunca podríamos pronosticar que llegaremos a cenar, si por mucho que conozcamos la velocidad a la que vamos a viajar, no conocemos el lugar desde el que iniciamos el viaje. En el caso de la atmósfera, la determinación del estado inicial exacto del sistema es bastante más complejo y supondría caracterizar la velocidad, temperatura, humedad, y demás propiedades de todas la porciones del mismo, lo cual es ciertamente complicado.

La caracterización del estado inicial de la atmósfera se basa en la recopilación de datos diversos a diferentes escalas espacio temporales. Existe una red mundial de observación, a partir de la cual se recopilan medidas de diferentes variables meteorológicas en distintas ubicaciones. La información que se obtiene a partir de esta red, es la base de conocimiento del tiempo presente, es decir, el estado inicial del sistema.

Las observaciones meteorológicas convencionales se efectúan a partir de estaciones meteorológicas ubicadas sobre el terreno en distintos puntos del globo. Estas estaciones contienen instrumental de medida, que permite registrar magnitudes físicas características del ambiente, como la temperatura, velocidad y dirección de viento, presión, humedad y otras. Aunque dependiente del tipo de estación y medida, es habitual registrar los datos en base horaria o diaria. Este tipo de medidas permite conocer el estado de la atmósfera junto al terreno. Para caracterizar el ambiente en altura se recurre habitualmente a instrumental sobre aviones y al lanzamiento de globos sonda. Los radiosondeos proporcionan medidas de temperatura, humedad y velocidad de viento a diferentes alturas a medida que ascienden, lo que permite disponer de perfiles atmosféricos en diferentes lugares del planeta. Este tipo de medidas suele efectuarse una o dos veces al día. Sobre los mares y océanos, la red de observación mundial la conforman diferentes tipos de boyas fijas o a la deriva, junto con instrumental a bordo de barcos que registran datos atmosféricos y oceanográficos como salinidad y temperatura del mar. Existen otro tipo de fuentes de adquisición de datos de forma remota, como son los satélites, radares, perfiladores, etc, que contribuyen al conocimiento del estado atmosférico. En estos casos, es habitual obtener el valor de la magnitud meteorológica de forma indirecta a partir de complejos cálculos sobre la magnitud física medida.

La recopilación de todos estos datos, adecuación de formatos, centralización y diseminación de lo mismos a todo el mundo es una tarea de la que se encargan diferentes organizaciones coordinadas por la Organización Meteorolológica Mundial (OMM).

Principales sistemas de adquisición de datos de la red mundial, estaciones automáticas, boyas, barcos, aviones, radares y satélites

Distribución de información meteorológica disponible para el análisis de las 12:00 de un día dado, se presentan los datos disponibles provenientes de estaciones, radiosondeos, boyas y barcos, aviones, satélites polares y geoestacionarios de arriba abajo izquierda a derecha respectivamente.

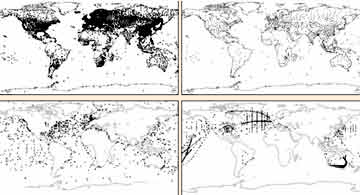
Un día cualquiera se recibe información proveniente de 5000 estaciones terrestres, 1000 sondeos, 2000 barcos y boyas, 600 aviones y otras fuentes (ver figura). Estas observaciones espaciadas de forma irregular, deben ser interpoladas a una malla, en base a distintos procedimientos y algoritmos de análisis con objeto de producir una rejilla regular de cobertura global.

Estos conjuntos de datos "enrejados" son producidos por distintos centros de predicción, de forma que cada profesional establece mallas con las configuraciones y datos necesarios para proceder a su inclusión como condiciones iniciales de los modelos numéricos de predicción operativos. Estas matrices de condiciones iniciales son la mejor estimación posible del estado inicial de la atmósfera para un tiempo determinado.

Hay distintos procedimientos que permiten, a partir de los datos directos e indirectos iniciales, interpolarlos a rejillas regulares. Estos procedimientos se llevan a cabo de forma automática. Hay una primera etapa en la que se procede al control de calidad de los datos disponibles, a partir de diferentes chequeos respecto de su validez por comparación con datos vecinos, con datos anteriormente registrados en ese mismo punto, chequeos de consistencia y otras técnicas que garantizan la validez de cada dato. A partir de ese conjunto de datos se procede a aplicar algún método de interpolación, de forma que podremos obtener los valores en los nodos de la rejilla establecida. Este tipo de procesos se aplica a todas las variables meteorológicas que caracterizan el estado atmosférico, a partir de procedimientos automáticos que se ejecutan varias veces al día, de modo que los análisis de los grandes centros meteorológicos suelen estar disponibles al menos dos veces al día.

Distribución de observaciones puntuales, enrejado aplicado y análisis con la distribución final de puntos.

Ejemplo de malla aplicada sobre un dominio que contiene al País Vasco.

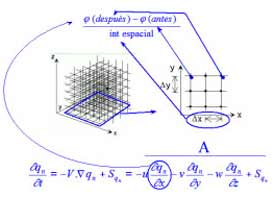
Las ecuaciones y su resolución

Los modelos numéricos de predicción del tiempo simulan dos aspectos fundamentales de la atmósfera, la dinámica del medio y los distintos procesos físicos que tienen lugar en su seno. La dinámica de un modelo concreto queda recogida a través de las ecuaciones de movimiento, mientras que la física de éste está representada a partir de distintas relaciones entre variables cuando la resolución es suficiente, bien de forma aproximada a partir de distintas parametrizaciones.

Las ecuaciones de movimiento determinan cómo las parcelas de aire se mueven de un lugar a otro como respuesta a las aceleraciones a las que se ven sometidas por la acción de diferentes fuerzas (gradiente de presión, coriolis, etc). Estas ecuaciones son las de Navier-stokes, una extensión de la 2ª ley de Newton (F=m.a) aplicada a sistemas continuos, que, junto con las leyes termodinámicas, conforman lo que se denominan ecuaciones primitivas del sistema. Este conjunto de ecuaciones simultáneas, no lineales en derivadas parciales no tiene solución analítica, por lo que debe ser resuelto de forma aproximada.

Ecuaciones primitivas y su interpretación.(primera parte)

Ecuaciones primitivas y su interpretación.(segunda parte)

Por su parte, los procesos físicos que recogen los modelos numéricos son la mezcla turbulenta, la precipitación, los procesos radiativos, la fricción y otros, dependiendo del tipo de modelo y de su resolución espacial. La precipitación en los modelos suele parametrizarse de forma diferente en función de si ésta se produce a una escala resoluble por el modelo o si se produce a escala subrejilla. El primer caso es el de la precipitación estratiforme, mientras que el segundo es el de la precipitación convectiva. Los procesos radiativos son parametrizados de forma que se representa las interacciones entre la radiación solar e infrarroja con las distintas capas de aire, dando cuenta del calentamiento o enfriamiento que se produce en presencia de agua en sus distintas fases. La turbulencia se parametriza de forma que refleja los movimientos que se producen a escala subrejilla responsables de transporte de diferentes magnitudes.

Vista de una malla con su alzado y perfil

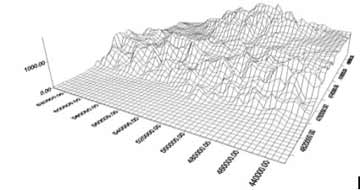
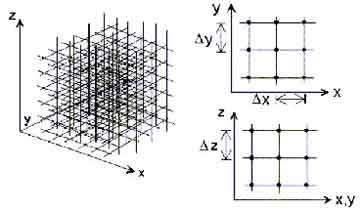
La resolución de las ecuaciones primitivas se acomete generalmente por el método de diferencias finitas, esta técnica numérica requiere del "enrejado" del dominio a simular. Este enrejado permite "discretizar" el continuo atmosférico de forma que podremos convertir las ecuaciones en derivadas parciales en ecuaciones de diferencias. Una vez conocidos los valores de todas las variables en el instante inicial en cada nodo de la rejilla, se puede proceder a la resolución numérica del sistema. El resultado será un conjunto de matrices con los variables de las distintas variables en cada punto de la rejilla para un tiempo futuro, es decir una predicción del tiempo.

Resolución mediante diferencias finitas: la predicción.

Resolución mediante diferencias finitas: la predicción.

En la práctica este método es el aplicado en los modelos denominados de área limitada (los que presentan bordes laterales), mientras que los modelos globales (los que no tienen bordes puesto que la hipotética rejilla es esférica y cerrada) suelen aplicar técnicas de resolución espectrales. En cualquier caso, estaremos hablando de la resolución de las ecuaciones en cientos de miles de puntos de rejilla, lo que requiere computadoras con gran capacidad de cálculo.

El postprocesado

Como hemos visto anteriormente el resultado de la predicción numérica no deja de ser una matriz de números con una estructura similar a la que tenia la matriz de condiciones iniciales. En la practica un conjunto de números en los cientos de miles de puntos en los que hemos discretizado el sistema a simular. En la práctica esta cantidad ingente de información debe ser correctamente formateada, tratada y almacenada para que sea de utilidad al predictor o analista humano. Los distintos centros meteorológicos se encargan de transformar la información que proporcionan la salida numérica en distintos productos. Es habitual proceder a la representación en planos horizontales de los diferentes campos meteorológicos de interés (presión en superficie, geopotenciales y temperaturas a diferentes niveles, precipitación acumulada, viento a distintos niveles y un largo etcétera).

Así mismo una vez superado el horizonte de predicción, los diferentes centros que ejecutan modelos predictivos, proceden a la validación del sistema. Para lo cual efectúan una comparación entre los resultados obtenidos (el estado atmosférico que se predijo) y los análisis disponibles (el estado atmosférico "real"), para lo cual es habitual disponer de sistemás automáticos que calculan diferentes estadísticos que indican la bondad del modelo en la predicción de diferentes parámetros.

Distintos mapas elaborados a partir de salidas de modelos numéricos.

Representaciones tridimensionales de las salidas numéricas.